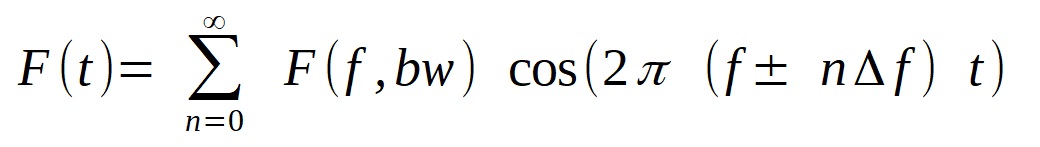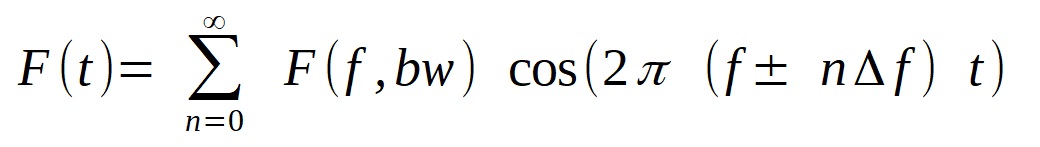1. Ultrashort Pulse
2. Pulse Wave
Every function
can be represented by the summation of individual
frequency components
, the so called
Fourier Series
. With a set of given single frequencies a new time signal can be generated.
On the other hand by
sampling
a time signal with respect to its frequency components, the
source frequencies
of the time signal can be revealed. This process is known under the term
Fourier Transformation
and widely used in engineering and science.
The
interactive visualization
on this pages exemplifies the Fourier Transformation and its characteristic parameters. The Graphs show; the resulting or starting time signal (top), the single frequency terms (bottom-left) and the spectral representation of the frequency components (bottom-right). The blue lines in the spectrum indicate the individual frequencies (
Delta Dirac Functions
); the connecting dark line is (spline-) interpolated.
The temporal spread of an optical ultrashort pulse lies in the range of picoseconds and below. In order to reach such short time regions, a broad spectrum of phase matched frequency terms is required. This is commonly achieved in mode-locked lasers. The relevant parameters responsible for the pulse shape are Δ frequency, center frequency, and bandwidth (frequency spacing); they can be adjusted with the control panel above.
In case of ideal mode-locking and zero dispersion the smallest possible pulse width (
Fourier Limited Pulse Width
) can be modeled as a fourier series of the individual frequency components.